Nilai x yang memenuhi (^4 log⁡ x)^2-x^2 log⁡√-3/4=0 adalah…

Nilai \(x\) yang memenuhi \( \displaystyle ({}^4 \! \log x)^2 - {}^2 \! \log \sqrt{x} - \frac{3}{4} = 0 \) adalah…

Pembahasan:

Penyelesaian dari soal ini, yaitu:

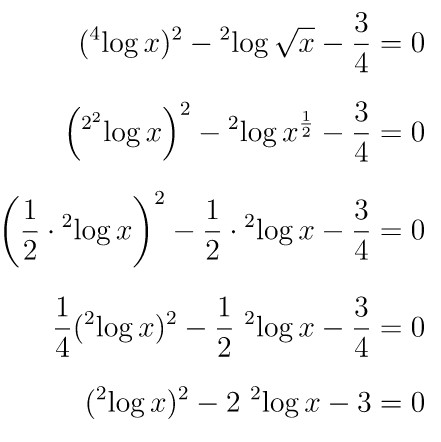
Sekarang misalkan \( {}^2 \! \log x = p \) sehingga persamaan di atas menjadi:

Untuk \(p = 3\), maka

\begin{aligned} {}^2 \! \log x = 3 \Leftrightarrow x = 2^3 = 8 \end{aligned}

Untuk \(p = -1\), maka

\begin{aligned} {}^2 \! \log x = -1 \Leftrightarrow x = 2^{-1} = \frac{1}{2} \end{aligned}

Jadi, nilai \(x\) yang memenuhi adalah 8 atau ½.

Jawaban D.

www.jagostat.com